Piano geometrico

Ricerca

Scuola

Titoli

PIANO PER DUE RETTE INCIDENTI

Home page

1. Premessa

2. Struttura dell'algoritmo grafico

3. Sviluppo dell'algoritmo grafico

4. Esercitazioni grafiche

4.1. Esercizio n° 1- Progressione dei passi

4.2.. Esercizio n°2- Progressione dei passi

1. PREMESSA

Poiché un piano resta individuato da due rette distinte che si intersecano in un punto X appartenente al piano, è necessario che si verifichi, a conclusione della procedura, la seguente legge di appartenenza e/o relativa contenenza.

[(r Ç s) = X Î a]

(r Ç s) Î a reciprocamente a Ì (r Ç s)

a Ì [X = (r Ç s)]

Assegnate, pertanto, due rette distinte, ma incidenti, collocate nello spazio del diedro, il problema si risolve sviluppando i passaggi sintetizzati nello schema sottostante del relativo algoritmo grafico.

Torna in alto

2. STRUTTURA DELL'ALGORITMO GRAFICO

Algoritmo grafico

Torna in alto

3. SVILUPPO DELL'ALGORITMO GRAFICO

Progressione dei passi dell'algoritmo grafico - esempio
Dati	Primo passo	Secondo passo	Terzo passo	Verifica	Risultato

Sviluppo dell’algoritmo	Operazioni grafiche relative
Dati	Torna in alto	Torna a esempio
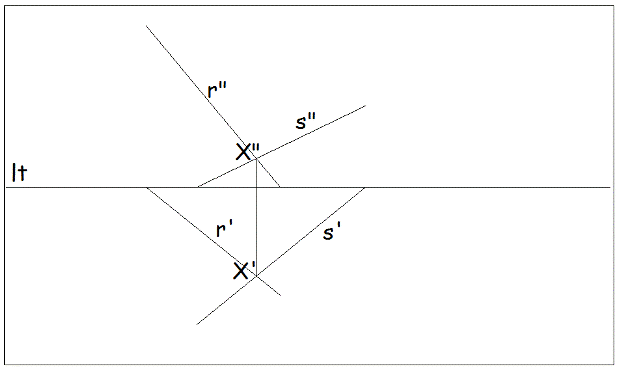
Siano assegnate le rette r(r’;r”) ed s(s’;s”) distinte e incidenti nel punto X (X’; X”) tali che in forma descrittiva sia:
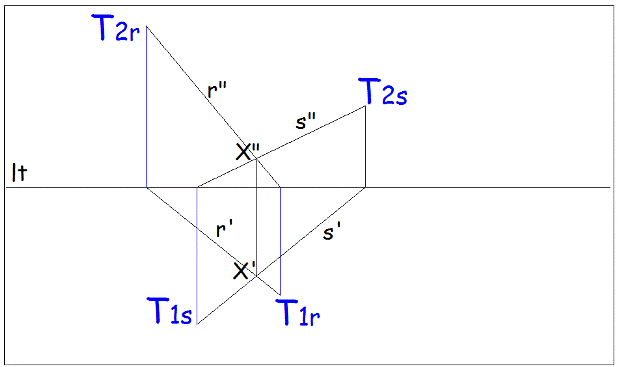
Primo passo	Torna in alto	Torna a esempio
Si ricorda che assegnate le proiezioni di una retta è facile determinarne le tracce partendo dai piedi di queste (incrocio della proiezione con la lt) per arrivare alle due proiezioni che le contengono.
Secondo passo	Torna in alto	Torna a esempio
Si ricorda che le tracce di un piano sono rette; inoltre per definire una retta necessita conoscere due punti. Nel nostro caso collegando (sommando) le due tracce prime si ottiene la traccia prima del piano a su p₁ e collegando (sommando) le due tracce seconde si ottiene la seconda traccia del piano a su p₂ come sintetizzato di seguito:
Passo terzo	Torna in alto	Torna a esempio
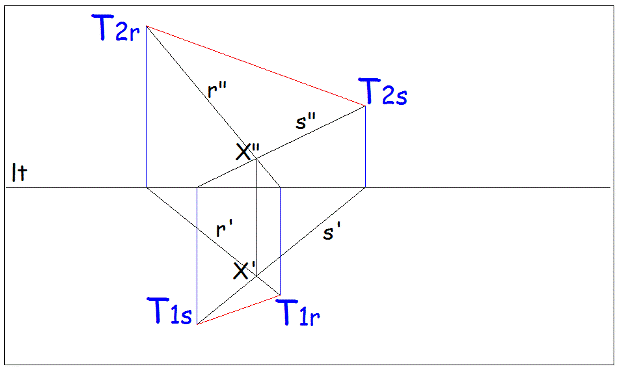
Le tracce del piano (t₁a) e (t₂a) sono rette reali ottenute come: Estendendo i segmenti di cui al passo precedente si determinano le due tracce (t₁a) e (t₂a) del piano passante per le due rette assegnate La verifica che le rette definiscano un piano si ha se le tracce intersecano la lt nel medesimo punto (punto unito alla lt). In alternativa le tracce devono essere parallele alla lt, significando che l’intersezione avviene in un punto improprio.
Verifica	Torna in alto	Torna a esempio
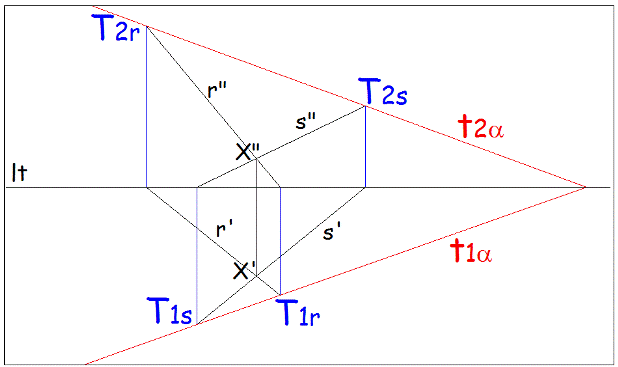
Definite le due tracce rappresentative del piano e controllato che si intersechino sulla lt nel medesimo punto, è necessario effettuare la verifica mediante la legge della contenenza tra piano e punto espressa come di seguito:
Risultato	Torna in alto	Torna a esempio
Eseguita la verifica con esito positivo si possono assumere le tracce del piano come gli elementi geometrici rappresentativi del piano passante per le due rette assegnate r ed s incidenti in X in quanto accade che: come era richiesto dal problema descrittivo

Torna in alto

ESERCITAZIONI GRAFICHE

Seguono due applicazioni grafiche con diverse tipologie di rette collocate in differenti diedri ed assegnate mediante le proiezioni.

Esercizio n° 1 - Progressione dei passi dell'algoritmo grafico
Dati1	Passo primo1	Passo secondo	Passo terzo1	Verifiche1	Risultato1

Esercizio n° 1 - Piano per due rette generiche incidenti collocate nel primo diedro
Esercizio 1 - Dati	Torna in alto	Torna a esercizio 1
Siano assegnate le proiezioni di due rette generiche r(r’; r”) ed s(s’; s”) collocate nel primo diedro ed incidenti nel punto X(X’; X”)
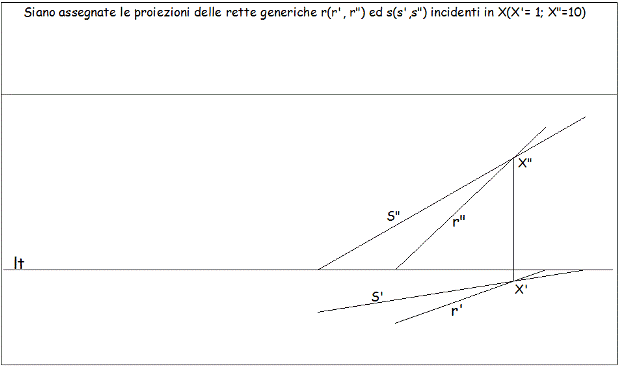Esercizio 1 - Passaggio1	Torna in alto	Torna a esercizio 1
Individuati i piedi delle tracce (intersezioni delle proiezioni con la lt) si determinano le tracce delle rette come punti reali uniti ai piani di proiezione e appartenenti alle rispettive proiezioni: (T₁rÎr'), (T₂rÎr”) (T₁sÎs'), (T₂sÎs”)
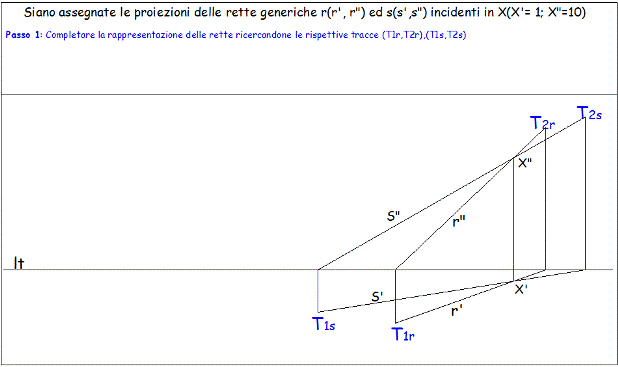Esercizio 1 - Passaggio 2	Torna in alto	Torna a esercizio 1
Definite le tracce delle due rette, collegando (T₁r +T₁s) si ottiene il segmento di retta relativo alla traccia del piano a su p₁, collegando (T₂r +T₂s) si ottiene il segmento di retta relativo alla traccia del piano a su p₂. In questo modo si determinano le direzioni delle due tracce del piano che per essere tali devono intersecare la lt nel medesimo punto (punto reale unito alla lt).
Esercizio 1 - Passaggio 3	Torna in alto	Torna a esercizio 1
Estendendo i due segmenti di retta di cui al passaggio 2, si determinano le rette (t₁a) e (t₂a) come tracce del piano a assegnato mediante due rette incidenti (r Ç s). Che le due rette sono tracce del piano è confermato d alla intersezione di queste con la lt nel medesimo punto.
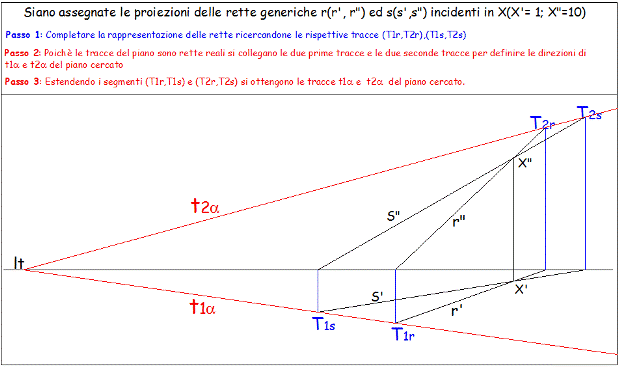Esercizio 1 - Verifiche	Torna in alto	Torna a esercizio 1
La verifica grafica, eseguita mediante le condizioni di appartenenza, risulta essere congruente sia con il problema geometrico (piano per due rette incidenti), sia con l’aspetto descrittivo (ricerca del tipo di piano), sia con l’aspetto rappresentativo (determinazione delle tracce del piano). Le due rette assegnate r ed s, infatti, appartengono al piano perché le rispettive tracce (due tracce prime e due tracce seconde) appartengono alle omonime tracce del piano (traccia prima di a e traccia seconda di a). Inoltre le due rette (r, s) sono incidenti perché le proiezioni del punto d’intersezione X (X’; X”) stanno nel medesimo luogo sulle proiezioni delle due rette r ed s perché il punto appartiene contemporaneamente ad entrambe le rette. Quindi resta completamente verificata la condizione:
Esercizio 1 - Risultato	Torna in alto	Torna a esercizio 1
Dallo studio delle tracce del piano possiamo risalire, poi, alla tipologia descrittiva del piano che si caratterizza come “piano generico nel primo diedro” avente le seguenti caratteristiche geometrico-descrittive

Torna in alto

Esercizio n° 2 - Progressione dei passi
Dati2	Primo passo2	Secondo passo2	Terzo passo2	Verifica2	Risultato2

Esercizio n° 2 - Piano per retta generica e retta frontale nel secondo diedro
Esercizio 2 - Dati	Torna in alto	Torna a esercizio 2
Siano assegnati i seguenti elementi geometrici tutti collocati nello spazio del secondo diedro. Retta frontale r (r’;r”), Retta generica s (s’;s”). Siano le due rette incidenti nel punto X (-X’; X”)
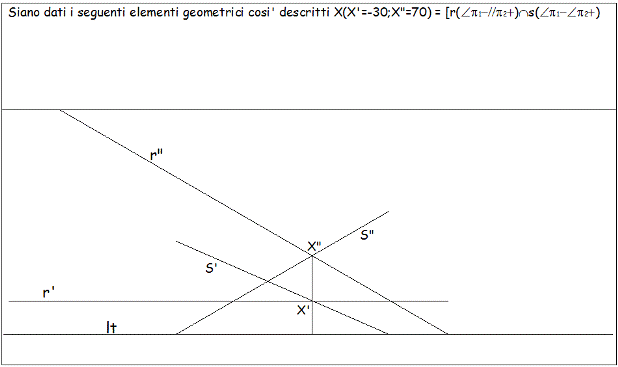Esercizio 2 – Passaggio 1	Torna in alto	Torna a esercizio 2
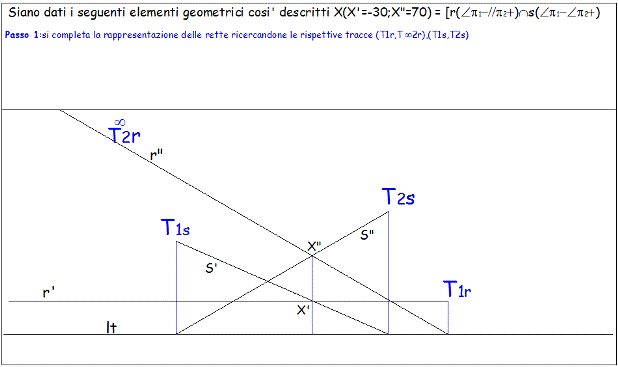Individuati i piedi delle tracce sulla lt si determinano le tracce delle rette come punti reali uniti ai piani di proiezione e appartenenti alle rispettive proiezioni: (T₁rÎr'), (T ^¥₂rÎr”) (T₁sÎs'), (T₂sÎs”) Da notare che essendo la retta r parallela a p⁺₂ la traccia seconda assume l’aspetto di un punto improprio indicato come T ^¥₂r
Esercizio 2- Passaggio 2	Torna in alto	Torna a esercizio 2
Definite le tracce delle due rette, collegendo (T₁r +T₁s) si ottiene il segmento di retta relativo alla traccia del piano a su p₁; conducendo per T₂s una semiretta parallela a r” si ottiene la direzione della traccia del piano a su p₂. Mi preme ricordare- a tal proposito- che al concetto di punto improprio deve esseresempre associato il concetto di parallelismo tra rette. In questo modo si determinano le direzioni delle due tracce del piano che per essere tali devono intersecare la lt nel medesimo punto (punto reale unito alla lt). Essendo la retta r una retta frontale nel secondo diedro la (T^¥2r) è un punto improprio, pertanto la t₂a si identifica, graficamente, mediante una retta parallela ad r” applicata nel punto reale T₂s.
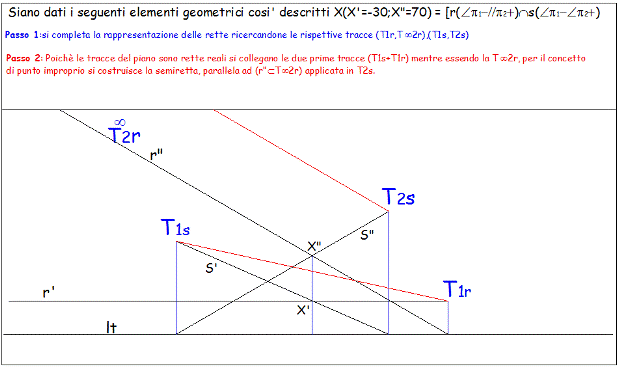Esercizio 2 – Passaggio 3	Torna in alto	Torna a esercizio 2
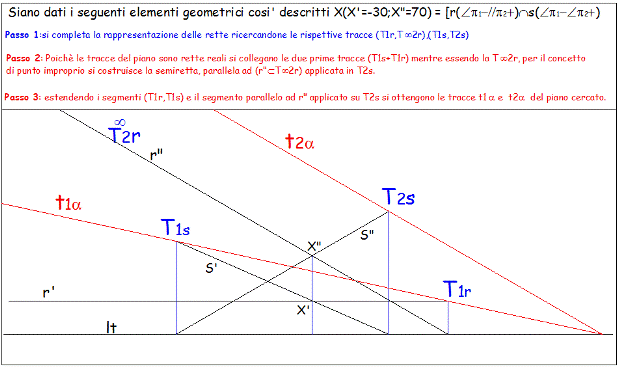Estendendo il segmento di retta (T₁r +T₁s) e la semiretta (T^¥₂r +T₂s), si determinano le rette (t₁a) e (t₂a) come tracce del piano a assegnato mediante le due rette incidenti (r Ç s). Che le due rette sono tracce del piano è confermato dalla intersezione di queste con la lt nel medesimo punto.
Esercizio 2 - Verifica	Torna in alto	Torna a esercizio 2
La verifica grafica, eseguita mediante le condizioni di appartenenza, risulta essere congruente sia con il problema geometrico (piano per due rette incidenti), sia con l’aspetto descrittivo (ricerca del tipo di piano), sia con l’aspetto rappresentativo (determinazione delle tracce del piano). Le due rette assegnate r ed s, infatti appartengono al piano perché le rispettive tracce (due tracce prime e due tracce seconde) appartengono alle rispettive omonime tracce del piano (traccia prima di a e traccia seconda di a). Inoltre le due rette (r, s) sono incidenti perché le proiezioni del punto d’intersezione X (X’; X”) stanno nel medesimo luogo sulle proiezioni delle due rette r ed s perché il punto appartiene contemporaneamente ad entrambe le rette. Quindi resta completamente verificata le condizione :
Esercizio 2 - Risultato	Torna in alto	Torna a esercizio 2
Dallo studio delle tracce del piano possiamo risalire, poi, alla tipologia descrittiva del piano che si caratterizza come “piano generico nel secondo diedro” avente le seguenti caratteristiche geometrico-descrittive.

Torna in alto